¿Por qué puede ganar nadal a federer en tierra batida? Indicadores determinantes del rendimiento en el juego.

Resumen

En este trabajo se realiza un análisis de los partidos que han enfrentado a Nadal y Federer en las finales de tierra batida de los torneos de la ATP. La muestra consiste en el partido final de los torneos de Roland Garros 2005, Montecarlo 2006, Roma 2006 y Roland Garros 2006. La metodología de investigación utilizada en este trabajo ha sido una observación sistematizada no participante en ambiente natural y además se ha elaborado un instrumento de observación ad hoc para este trabajo. El análisis de los datos se basa en la regresión logística. La variable dependiente se refiere al ganador de cada uno de los puntos de cada partido. Las variables independientes son el número de intercambios en cada punto, el tiempo de partido y la acción técnica de finalización del punto: saque, derecha, revés, volea, dejada, remate y globo. Los resultados empíricos permiten justificar que cuanto mayor es el número de intercambios más probabilidades tiene de ganar el punto Nadal y menos Federer y que las acciones técnicas determinantes para el resultado del partido son: el error no forzado de volea, de derecha y de revés, en donde Federer tiene peor rendimiento que Nadal. En cambio, en la volea ganadora Federer tiene más probabilidades de ganar el punto que Nadal. Además, se analizan las zonas de campo donde se produce la finalización del punto para cada jugador.

1. Introducción

El objetivo de este trabajo consiste en analizar el perfil del juego de Nadal y Federer en la superficie de tierra batida para comprender cuáles son los factores que pueden ocasionar la victoria de uno u otro. La unidad de análisis que se ha adoptado consiste en cada uno de los puntos que conforman cada partido. Si bien el marcador final del partido es, desde luego, la variable clave para determinar el éxito en el juego a veces la valoración exclusiva del juego por su resultado final puede impedir valorar otros aspectos del comportamiento de los jugadores. Y es que, por ejemplo, rendimiento y resultado en ocasiones no son lo mismo. Se puede ganar demostrando un rendimiento inferior al habitual por parte de un jugador y se puede perder actuando por encima de lo acostumbrado. Además resulta preciso diferenciar facetas del juego porque es posible que, por ejemplo, para un jugador en un partido el juego desde el fondo de la pista sea óptimo y el juego en la red sea deficiente. Una correcta evaluación del rendimiento en el juego pu3ede permitir identificar potenciales campos de mejora en los jugadores. En ese contexto se enmarca este trabajo. La investigación se estructura del siguiente modo. Una vez presentados los objetivos, se explica la metodología planteada en el trabo A continuación, se prueba esta metodología en el análisis de los partidos que han enfrentado sobre tierra batida a Nidal y Federer. En último lugar, se destacan los principales conclusiones del trabajo.

2. Materia y método

Muestra La muestra consiste en las finales disputadas en tierra batida por Nadal y Federer en los torneos de la ATP. Las finales analizadas son Roland Garros 2005, Montercarlo 2006, Roma 2006 y Roland Garros 2006. El número total de observaciones es de 1118 puntos. En la Tabla 1 se presenta esta información.

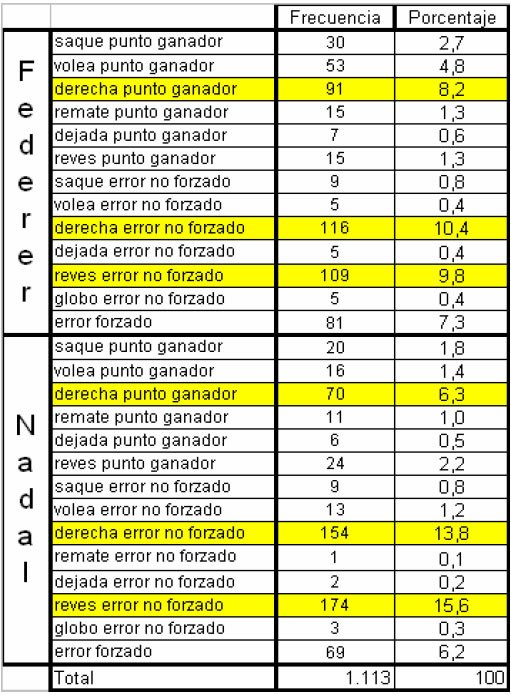
Tabla 1. Partidos analizados y número total de observaciones recogidas.

Instrumento El instrumento, elaborado ad hoc, es un formato de campo construido a partir de los siguientes criterios: Torneo, Set, Número de intercambios, Final de punto, Zona, Punto ganador, Tiempo de partido y Ganador del partido. El formato de campo se presenta esquemáticamente en la Tabla 2.

Tabla 2. Formato de campo sobre el desarrollo del juego en el tenis.

Procedimiento Todo el registro se ha realizado a partir del análisis de cintas grabadas. Las cintas de las que hemos dispuesto para la realización del estudio han sido grabadas en vídeo VHS desde la emisión realizada por una cadena de televisión. La imagen registra la evolución espacial del juego siguiendo en todo momento al jugador que golpea a la pelota y su actuación sobre la misma. La metodología de investigación para el desarrollo del presente trabajo ha sido una observación sistematizada no participante en ambiente natural. De cada secuencia del juego se registraban los siguientes criterios descriptivos: Torneo, Set, Jugador que inicia al punto, Número de intercambios, Final del punto, Zona, Punto ganador, Tiempo de partido y Ganador del partido. La observación y el correspondiente registro ha sido realizado por un equipo de tres observadores entrenados específicamente para este estudio. El control de la calidad del dato se ha efectuado desde una perspectiva cuantitativa y cualitativa. En primer lugar, se produjo la formación de los observadores, todos ellos licenciados en educación física, durante una semana. Al finalizar este proceso, se efectuó un control de la concordancia interobservador mediante la aplicación del coeficiente Kappa de Cohen. En todos los caos el Kappa de Cohen superó el valor de 0,90. Posteriormente, cada observador registró un partido. A continuación se seleccionó al azar uno de los partidos que fue nuevamente visionado. El kappa de Cohen alcanzó el valor 0,98. Variable dependiente La variable dependiente es el resultado alcanzado en cada punto de cada partido de las finales de los torneos disputados en tierra batida de Roland Garros 2005 Montecarlo 2006, Roma 2006 y Roland Garros 2006, pudiendo ser ganado por Nadal o Federer. Como se trata de una variable dicotómica, el valor 1 se referirá a un punto ganado por Nadal y el 0, por Federer. Variable independiente Las variables independientes incluidas en el estudio son las siguientes. En primer lugar, se ha introducido una variable para identificar la duración de los puntos de cada partido. La variable intercambios se refiere al número de veces que los jugadores han golpeado la bola dentro del mismo punto antes de finalizar la acción. Así, un valor de 6, significará que ha habido 6 intercambios de la bola antes de que el punto finalizase. El efecto esperado para esta variable es el siguiente: cuantos más intercambios tiene un punto más probabilidad tiene de ganarlo Nadal y viceversa, cuanto menos intercambios hay más posibilidades de ganar el punto tiene Federer. La segunda variable de control se refiere a que es posible que el tiempo de partido pueda tener influencia sobre el resultado del partido. Para ello hemos medido la duración del partido en cada momento de la siguiente forma: el valor 0 se refiere a un punto del partido cuando éste tiene una duración de 0 a 1 hora, el valor 1 refleja un punto que se ha sucedido cuando el partido estaba en una duración de 1 a 2 horas; el valor 2 a una duración de 2 a 3 horas y, finalmente, el valor 3 a una duración de más de 3 horas. El efecto esperado es el siguiente: conforme la duración del partido es mayor, más probabilidad tienen de ganar el punto Nadal y viceversa. La tercera variable recoge la acción que ha dado pie a la finalización del punto y que puede ser saque punto ganador, volea punto ganador, derecha punto ganador, remate punto ganador, dejada punto ganador, globo punto ganador, saque error no forzado, volea error no forzado, derecha error no forzado, remate error no forzado; dejada error no forzado, globo error no forzado, error forzado y conjunto vacío para aquellas acciones inobservables o de imposible concreción. La acción de finalización que se ha tomado como categoría de referencia para cuantificar el resto de variables que identifican a las acciones del juego es el saque punto ganador. Los estadísticos descriptivos de estas variables se presentan en la Tabla 2.

Tabla 2. Estadísticas descriptivas de las variables analizadas.

Análisis estadístico En el análisis de la influencia de las variables seleccionadas sobre el resultado de los puntos en cada partido: i 1 2 i 3 i 4 i i RE = ? +? ? INT +? ?TEM +? ? FP +? [1] donde RE es el resultado del punto pudiendo ser ganado por Nadal (valor 1) o Federer (valor 0); (INT), es el número de intercambios que se han producido en el punto hasta su finalización, (TEM) es el tiempo de partido y (FP) es el tipo de finalización del punto

3. Resultado y discusión

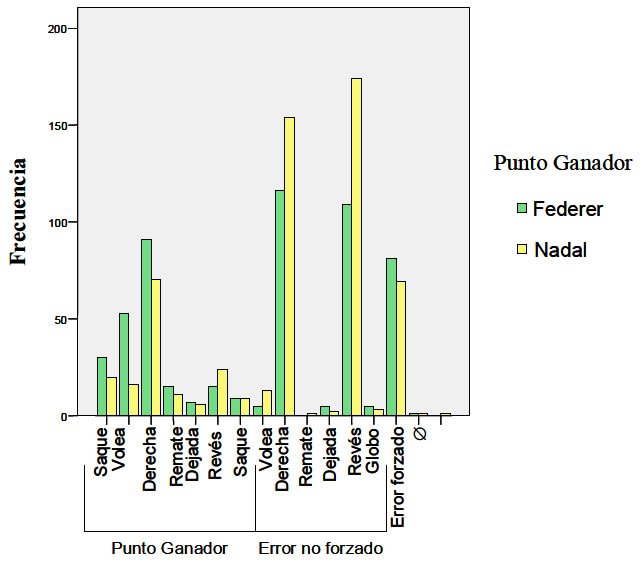
En la Tabla 3 se presenta el origen de los puntos ganados por Federer y Nadal en los partidos analizados. Se destaca aquellas acciones que para cada jugador son más importantes dentro de su modelo de juego. Como puede apreciarse, para Federer los puntos ganados con la derecha y los errores no forzados cometidos por Nadal con su derecha y revés son las acciones que tienen más relevancia en su juego. Para Nadal, al igual que para Federer, las acciones más positivas de juego más importantes son su derecha y los errores no forzados cometidos por Federer con su derecha y revés. En cualquier caso, destaca que Federer comete más errores no forzados que Nadal y que, por el contrario, obtiene más puntos con su derecha. En la Figura 1 se compara de forma gráfica el origen de los puntos ganados por Federer y Nadal en los partidos analizados, intentando demostrar modelos de rendimiento diferentes para cada jugador.

Tabla 3. Origen de los puntos ganados por Federer y Nadal.

Figura 1. Comparación del perfil de juego para Federer y Nadal.

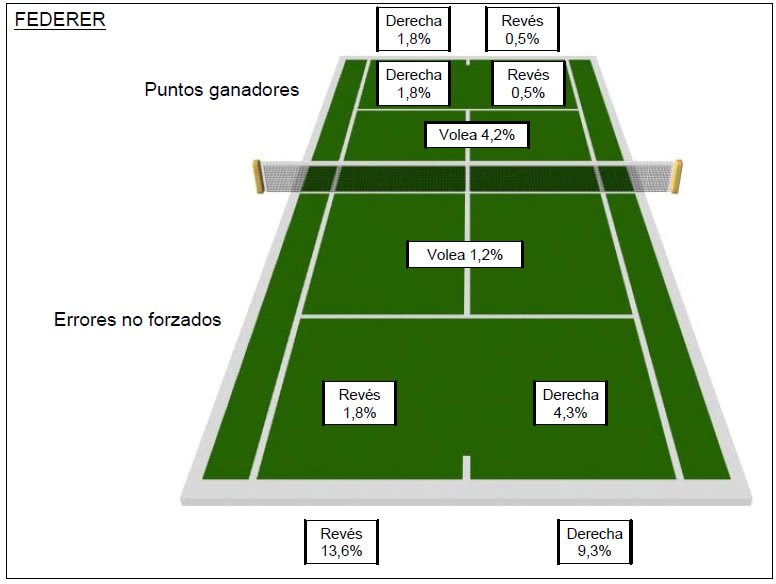
En la Tabla 4 se analiza la zona del campo desde la que se originan los puntos ganados por cada jugador. Para ello hemos diferenciado el espacio en tres zonas: la zona 1 ocupa la zona posterior a la línea de fondo, la zona 2 va desde la línea de fondo hasta la línea media del campo propio de cada jugador y la zona 3 va desde el final de la zona 2 hasta la red. Al igual que en las Tablas 2 y 3 se destacan los datos más destacados para cada jugador.

Tabla 4. Zonas de origen de los puntos ganados por Federer y Nadal.

Esta misma información se presenta en las Figuras 2 y 3: Se intenta reflejar las zonas preferenciales de los puntos ganadores y los errores no forzados por parte de Federer y Nadal. Únicamente se presentan las acciones más significativas para cada jugador.

Figura 1. Zona preferenciales de los puntos ganadores y los errores no forzados de Federer.

Figura 2. Zona preferenciales de los puntos ganadores y los errores no forzados de Nadal.

La influencia de las variables tomadas en consideración sobre el resultado de los puntos analizados que se ha deducido en el apartado anterior se ha estimado a través de logit binomial, dada la naturaleza de la variable dependiente (esto es, categorías cualitativamente distintas). Con la función logit binomial se puede estimar para Federer y Nadal la probabilidad de ganar un punto del partido frente a la probabilidad de perder. Los resultados del modelo se presentan en la Tabla 5. En la primera columna de la Tabla 5 se leen los nombres de las variables independientes incluidas en el modelo. Conviene recordar que tanto el cálculo como la interpretación de los coeficientes del logit binomial han de hacerse en términos relativos, es decir, contrastando siempre dos categorías concretas de la variable dependiente. La segunda columna de la Tabla 5 proporciona los parámetros estimados por logit binominal con sus errores típicos correspondientes entre paréntesis para el contraste entre la probabilidad de Federer y Nadal de perder frente a ganar en los puntos de los partidos observados. Como se deduce de la Tabla 5, la variable intercambios es estadísticamente significativa al 1 por 100 y apunta en el sentido esperado: cuantos más intercambios hay, mayor probabilidad de ganar el punto tiene Nadal y menos Fededer. La variable tiempo de partido no es estadísticamente significativa para explicar la probabilidad de ganar los puntos del juego por parte de Nadal o Federer. Es decir, da igual que el punto analizado se produzca al inicio o al final del partido. No es relevante. Quizás la variable intercambios recoja mejor la hipótesis de que la duración del juego puede resultar más favorable para Nadal que para Federer. En la extensión final del partido quizás influyan más aspectos que los directamente relacionados con la duración de los puntos: discusiones, interrupciones del público, descansos,… Finalmente, en lo que se refiere a la acción que ha dado pie a la finalización del punto hasta 5 categorías presentan diferencias estadísticamente significativas con respecto a la acción de finalización tomada como referencia que es el saque punto ganador. Federer tiene más probabilidad de obtener puntos ganadores a través de la volea que Nadal. Si embargo, en las acciones de volea error no forzado, derecha error no forzado, remate error no forzado y revés error no forzado es Federer el que tiene más probabilidades de cometer fallos que Nadal. De este modo, parece posible identificar las facetas del juego más importantes o con mayor probabilidad de decantar el resultado de los puntos hacia un jugador u otro. Resultaría interesante comprobar si estas mismas acciones de finalización son las que expresan el éxito en el juego en otras superficies.

Tabla 5. Variables determinantes en el resultado de los puntos en los partidos en tierra batida entre Nadal y Federer.

4. Conclusiones

En este trabajo hemos analizado los partidos que han enfrentado a Nadal y Federer en las finales de tierra batida de los torneos de la ATP. Los resultados empíricos permiten justificar que cuanto mayor es el número de intercambios más probabilidades tiene de ganar el punto Nadal y menos Federer y que las acciones técnicas determinantes para el resultado del partido son: el error no forzado de volea, de derecha y de revés, en donde Federer tiene peor rendimiento que Nadal. En cambio, en la volea ganadora Federer tiene más probabilidades de ganar el punto que Nadal. La duración del partido no es una variable estadísticamente significativa. Además, hemos analizado los perfiles de actuación de ambos jugadores y las zonas de actuación preferencial en el espacio de juego.

Bibliografía

• Hughes, M.D.; Bartlett, R. (2002). The use of performance indicators in performance analysis. Journal of Sports Sciences, Special Edition, 20, 739-754.
• Hughes, M.D., Evans, S.; Wells, J. (2001). Establishing normative profiles in performance analysis. International Journal of Performance Analysis of Sports, 1, 1-25.
• McGarry, T., Franks, I. (1994). A stochastic approach to predicting competition squash match-play, Journal of Sports Science, 12, 573-584.
• Neville, A.; Atkinson, G.; Hughes, M., Cooper, S.M. (2002). Statistical methods for analysing discrete and categorical data recorded in performance analysis. Journal of Sports Science. 20.829-844.
• O´Donoghue, P. (2005). Normative profiles of sports performance, International Journal of Performance Analysis in Sport, 5, 1, 104-119.
• White, H. (1980). A Heterokedastic-Consistent Covariance Matrix Estimator y a Direct Test for Heterokedasticity, Econometrica, 48, 817-838.